Bir kalite izleme diyagramı olan kontrol diyagramı, bir süreçteki değişimin incelenmesine ve normal olmayan değişikliklerin belirlenmesine yarayan, ilk olarak Walter Andrew Shewhart tarafından 1924 yılında geliştirilen grafik araçlardır.

İnsanın etkisi ile meydana gelen tüm olaylarda değişkenlik söz konusudur. Bu sebeple üretim süreçlerinde çeşitli nedenlerin etkisi sonucunda değişkenliğin ortaya çıkması doğaldır. Temel amacı üretim sürecini kontrol altında tutmak olan kalite kontrol faaliyetlerinin, istatistiksel yöntemlerle ve güvenilir biçimde gerçekleştirilebilmesi ancak kontrol diyagramları ve her bir prosesin kontrol altına alınabilmesi ile gerçekleştirilebilir.

Türleri

Kabul kontrol diyagramları

Belirli bir boyut için mühendislik toleransı, imalat prosesinin, doğal dağılımını aştığı takdirde farklı bir X- diyagramı kullanılarak prosesin kusurlu yüzdesinin kontrol altında kalmasına çalışılmaktadır. Bu durumda kontrol diyagramının limitleri proses ortalamasının standart düzeyi yerine mamulün spesifikasyon limitlerine dayalı olmaktadır. Örnek ortalaması bu limitler içinde kaldığı sürece, proses kabul edilebilir varsayılacaktır.

Proses ortalamasının sabit kaldığı varsayımı ortadan kalkacak ve bu değişmeler, istenmeyen düzeyde kusurlu parça yüzdesi imaline yol açan bir proses ortaya çıkmadıkça, proses ortalamasının spesifikasyon limitleri içinde değişmeler göstermesine izin verilecektir. Bu türden X diyagramları “kabul kontrol diyagramları” olarak isimlendirilmektedir.

Birikimli toplam kontrol diyagramları

Birikimli toplam kontrol diyagramları, temel olarak bir prosesin sürekli kontrolünün sağlanması amacıyla kullanılmaktadır. Shewhart diyagramlarına karşı başlıca üstünlüğü, daha düşük maliyette aynı etkinliği sağlamasıdır. Özellikle değişimin fazla büyük olmadığı durumlarda, proses ortalamasındaki ani ve ısrarlı değişme birikimli toplam kontrol diyagramlarında derhal fark edilmekte, değişmenin zamanı daha belirgin olarak saptanabilmekte ve gösterilebilmektedir. Birikimli toplam kontrol diyagramlarında herhangi bir karara varılırken verilerden elde edilen bilgilerin tümünün kullanılması gerekmemektedir.

Fonksiyonu

Kontrol diyagramları incelenen sürecin ne derece kontrol edilebilir olduğunu göstermek için ve sapmalardaki genel sebepleri özel sebeplerden ayırmak için kullanılır. Çünkü kontrol diyagramları ile belirlenen üst ve alt kontrol limitleri arasındaki alan, alınan örnekteki değişkenliğin genel bir sebepten olduğunu gösterir. Genel sebepler kontrol altında tutulmasına olanak olmayan ve sürecin kendiliğinden kaynaklanan nedenler olup sürece olan etkisi büyük değildir.

Özel sebepler ise düzeltilmesiyle değişkenliğin azalacağı ve sürecin kontrol altında tutulabileceği sebeplerdir. Ayrıca kontrol diyagramları sayesinde üst ve alt kontrol limitleri dışında kalan noktaların özel nedenlerden kaynaklandığı bilinir ve bu özel nedenler için gerekli önlemler zamanında alınarak çıkacak kalite problemleri önlenmiş olur. Bunun dışında, kontrol diyagramları ile noktaların limitler arasında kalması sağlandığından kontrol edilecek parça sayısı dolayısıyla kalite maliyeti azalır.

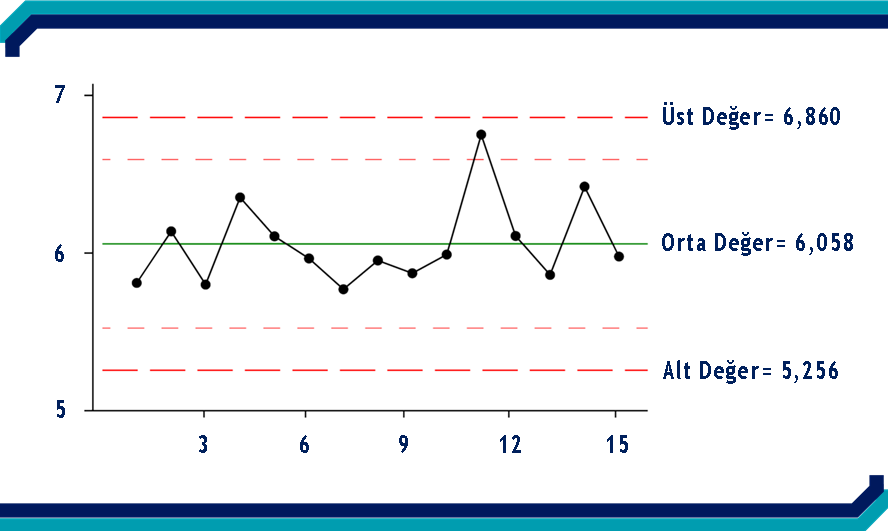
Şekildeki kontrol diyagramında ölçülen kalite karakteristiğinin farklı örnek hacimlerindeki değişimi görülmektedir. Alt sınır 5,256 üst sınır 6,860 ve orta değer 6,058’dir. Ölçülen kalite karakteristiği değerleri bu alt ve üst limit arasında değişmektedir.

Çeşitleri

İncelenecek kalite karakteristiği için alınan örnek sayısal olarak ifade edilebiliyorsa kullanılabilecek kontrol diyagramı çeşitleri x ̅ , R ve s grafikleridir. Eğer veriler ölçülemiyor ancak hissedilebiliyorsa p, np, c ve u çizelgeleri kullanılır.

Kullanımı

Kontrol diyagramı oluşturmak için öncelikle iyileştirilecek kalite karakteristiği hakkında verilere sahip olunması gerekir. Bu veriler tekrar eden işlemlerin sürekli olarak ölçülmesiyle olacaktır. Alınan verilerin standart sapmasının ve aritmetik ortalamasının bulunması ikinci adımdır. Bundan sonraki işlem standart sapma ve ortalama kullanılarak üst ve alt kontrol limitlerinin bulunmasıdır. Üst ve alt kontrol limitleri ortalama ± 3 σ formülünden bulunur.

Sıradaki işlem bulunan değerlerin grafiğe aktarılmasıdır. Grafikte 3 çizgi vardır. Orta çizgi kalite karakteristiğin hedeflenen değeri ile ilgili olup ortalamanın yazıldığı çizgidir.